Quelle: FML Magazin 012 Dezember 2023
GEOMETRIA PERENNIS Kap. 4
Stellt Euch einmal vor, er ginge verloren. –
Wer ginge verloren???
Na er, der Py, der Pythagoras.
Lebte der nicht vor etwa 25 Jahrhunderten und ist damals verstorben?
Ja, aber den meinte ich nicht. Ich sprach von dem Lehrsatz und ich meinte auch nicht irgend einen von den unzählbaren Tripeln aus der Menge der
a2 + b2 = c2, sondern den mit
3, 4 und 5,
den von der Schule, den, von dem den Schülern fast alles verschwiegen wird, weil auch die Lehrer nicht bescheid wissen.
Ja und was wäre dann, es wäre doch eine enorme Erleichterung für die Schüler, sich mit diesem Unfug nicht mehr herumplagen zu müssen. –
Stellt Euch vor: Für 1.000 Jahre wäre er weg, niemand weis mehr etwas von ihm, aber das Stomachion des Archimedes hätte überdauert. –
Ja und?
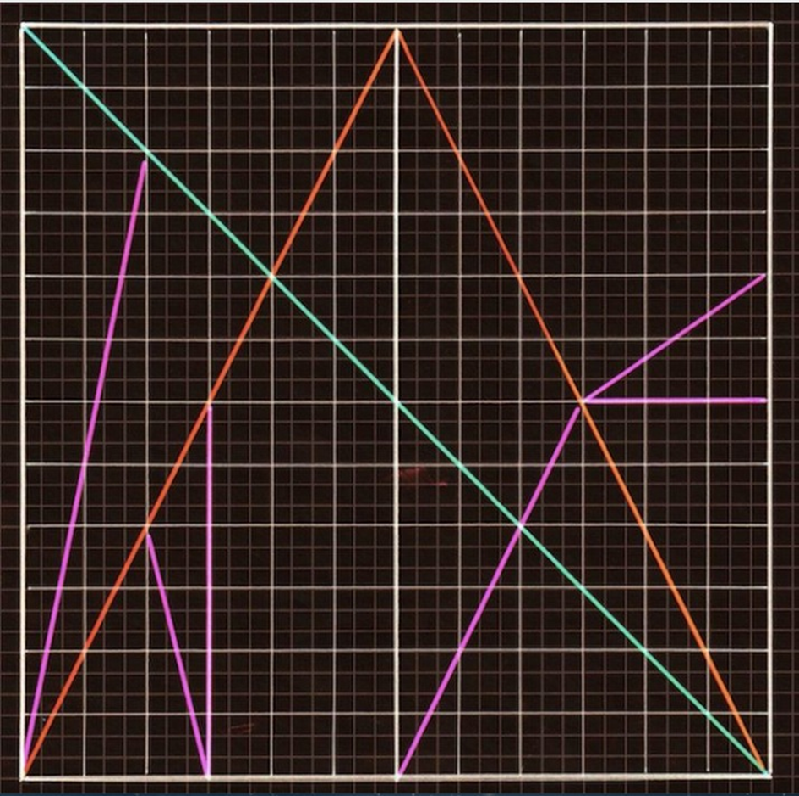
Archimedes hat da auch das „Dreieck im Quadrat“ thematisiert. Zweimal die Schlüssel-Strecke für die Proportionen des Goldenen Schnittes. In der Mitte des Quadrats laufen sie oben spitz zusammen und an den unteren Ecken des Quadrats enden sie. Neben vielem anderen sind sie auch die Schlüssel für den
Py mit 3, 4 und 5
in dem großen rechtwinkligen Dreieck. Dazu bedürfte es einer dritten Strecke gleicher Länge von der linken unteren Ecke zur Mitte der rechten Seite und das alt ehrwürdige Dreieck wäre wieder hergestellt.
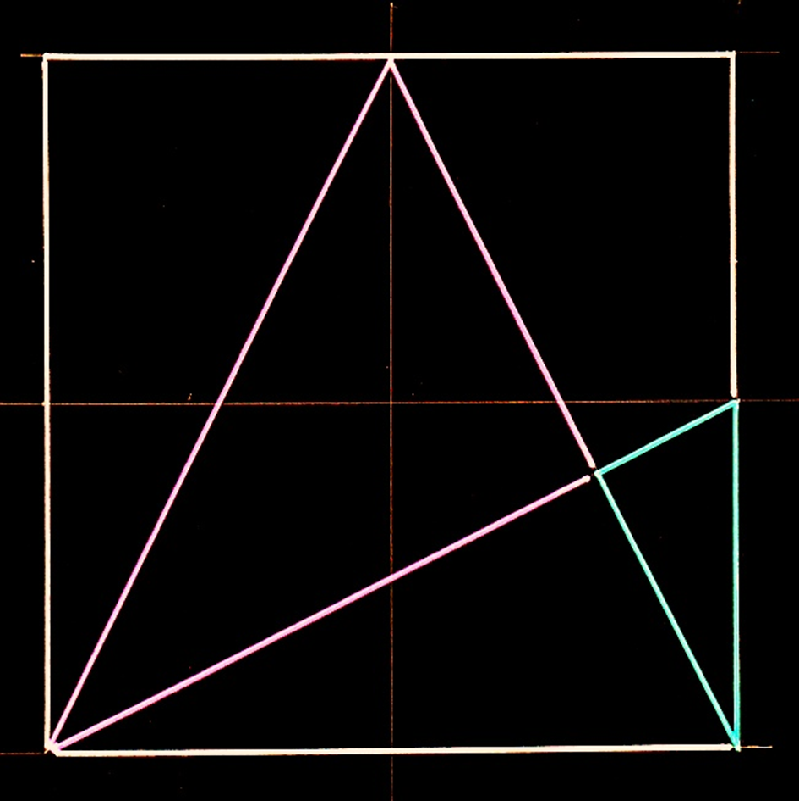
Und klein, rechts unten wäre dann auch wieder dieses halbe Rechteck im Seitenverhältnis von 1 zu 2 und mit der Hypotenuse, mit der √5.
Das ist in der Formensprache des Geometrischen die göttliche Schöpfungsgeschichte, die unser großer Bruder Platon einst noch gekannt hat. Im Buch Politeia finden wir sie, als Hochzeitszahl (St.-Zählung 645) verschlüsselt zwar und zusätzlich von Interpreten verkorkst, aber trotzdem unverkennbar.





